Pythonのルンゲクッタ法について

2025年6月4日

ルンゲ＝クッタ法（Runge-Kutta法）は、常微分方程式（ODE）の数値的な解法のひとつで、特に初期値問題において広く用いられる方法です。

Pythonでルンゲ＝クッタ法を使う際は、基本的な自作コードから、scipy.integrate.solve_ivp()のようなライブラリの活用まで様々な方法があります。

ルンゲ＝クッタ法とは？

常微分方程式の初期値問題

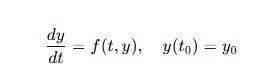
を数値的に解く方法で、オイラー法の高精度版とも言えます。

特徴

高精度（特に4次ルンゲ＝クッタ法：RK4）
解の安定性が高い
1ステップあたりの計算量は多いが、精度が高いためステップ数を減らせる

ルンゲ＝クッタ法の仕組み（4次）

4次ルンゲ＝クッタ法（RK4）は次のようなアルゴリズムで進みます。

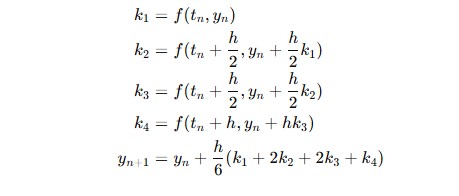
h：ステップ幅
f(t,y)：導関数（微分方程式）
yn+1：次のステップの値

Pythonでの実装例（RK4）

例えば次の微分方程式

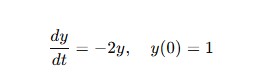
これをPythonでRK4法を用いて解いてみましょう。

import numpy as np
import matplotlib.pyplot as plt

# 微分方程式 dy/dt = f(t, y)
def f(t, y):
    return -2 * y

# ルンゲ＝クッタ4次法
def runge_kutta_4(f, y0, t0, t_end, h):
    t_values = [t0]
    y_values = [y0]
    
    t = t0
    y = y0
    while t < t_end:
        k1 = f(t, y)
        k2 = f(t + h/2, y + h*k1/2)
        k3 = f(t + h/2, y + h*k2/2)
        k4 = f(t + h, y + h*k3)
        
        y += h * (k1 + 2*k2 + 2*k3 + k4) / 6
        t += h

        t_values.append(t)
        y_values.append(y)
    
    return np.array(t_values), np.array(y_values)

# パラメータ設定
t0 = 0
t_end = 5
y0 = 1
h = 0.1

# 実行
t_vals, y_vals = runge_kutta_4(f, y0, t0, t_end, h)

# グラフ表示
plt.plot(t_vals, y_vals, label='RK4 approximation')
plt.plot(t_vals, np.exp(-2*t_vals), 'r--', label='Exact solution')
plt.xlabel('t')
plt.ylabel('y(t)')
plt.title('Runge-Kutta Method vs Exact Solution')
plt.legend()
plt.grid(True)
plt.show()

SciPyでの利用（実務向き）

実際のプロジェクトでは、自作よりライブラリの使用が推奨されます。

PythonのSciPyライブラリに含まれるsolve_ivp()関数は、ルンゲ＝クッタ法（明示的なRK法）を内部に実装しています。

from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt
import numpy as np

def f(t, y):
    return -2 * y

sol = solve_ivp(f, [0, 5], [1], method='RK45', t_eval=np.linspace(0, 5, 100))

plt.plot(sol.t, sol.y[0], label='solve_ivp (RK45)')
plt.plot(sol.t, np.exp(-2 * sol.t), 'r--', label='Exact solution')
plt.legend()
plt.grid(True)
plt.show()

RK45：デフォルト。Dormand-Prince法（5次精度、4次エラー評価付き）
他にも RK23, DOP853, Radau, BDF なども使用可能

まとめ

特徴	内容
精度	RK4は非常に高精度（中規模の問題では十分）
実装のしやすさ	手動実装も可能だが、SciPy等を使う方が実務向き
適用範囲	初期値問題に最適。剛性問題には不向き（BDF法などを使用すべき）
欠点	ステップサイズを間違えると不安定に（安定性領域を超えると発散する）

以上、Pythonのルンゲクッタ法についてでした。

最後までお読みいただき、ありがとうございました。

よかったらシェアしてね！