PythonのSciPyを用いた補間方法について

2025年6月23日

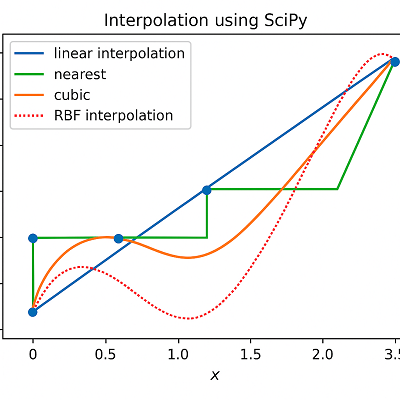
SciPy（Scientific Python）は、数値計算や信号処理、統計処理などを行うための強力なライブラリで、その中にある scipy.interpolate モジュールは補間（interpolation）を行うための機能が豊富に用意されています。

補間は、離散的なデータから連続的な関数を推定する方法で、機械学習、信号処理、物理シミュレーションなど多くの分野で重要です。

SciPyでの補間の基本的な方法と分類

1次元補間（`interp1d`）

最も基本的な補間関数です。

等間隔でも非等間隔でも補間できます。

使い方

from scipy.interpolate import interp1d
import numpy as np
import matplotlib.pyplot as plt

x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 1, 0, 1, 0])

# 線形補間
f_linear = interp1d(x, y, kind='linear')

# 補間点を生成
xnew = np.linspace(0, 4, 100)
ynew = f_linear(xnew)

plt.plot(x, y, 'o', label='original data')
plt.plot(xnew, ynew, '-', label='linear interpolation')
plt.legend()
plt.show()

`kind` パラメータの種類

'linear': 線形補間（デフォルト）
'nearest': 最近傍補間
'zero': ゼロ次ステップ関数補間
'slinear': 区間ごとの線形補間（線形スプライン）
'quadratic': 2次スプライン
'cubic': 3次スプライン（滑らか）
'previous'/'next': 前方/後方補間（階段状）

スプライン補間（`UnivariateSpline`, `CubicSpline`）

より滑らかな補間を得るために使います。

スプラインは、関数を滑らかにつなぐ多項式の組です。

`UnivariateSpline`（スムージング可）

from scipy.interpolate import UnivariateSpline

x = np.linspace(0, 10, 10)
y = np.sin(x) + np.random.normal(0, 0.1, x.shape)

spl = UnivariateSpline(x, y)
xnew = np.linspace(0, 10, 1000)
ynew = spl(xnew)

plt.plot(x, y, 'o', label='data')
plt.plot(xnew, ynew, label='spline')
plt.legend()
plt.show()

s=0 で厳密に通るスプライン補間、s>0 でスムージング（ノイズ除去）も可能。

`CubicSpline`（厳密な3次スプライン）

from scipy.interpolate import CubicSpline

cs = CubicSpline(x, y)
y_cs = cs(xnew)

plt.plot(x, y, 'o', label='data')
plt.plot(xnew, y_cs, label='Cubic Spline')
plt.legend()
plt.show()

2次元・多次元補間（`griddata`, `RBFInterpolator`など）

`griddata`（2Dデータの補間に便利）

from scipy.interpolate import griddata

# サンプルデータ
points = np.random.rand(100, 2)
values = np.sin(points[:, 0] * 2 * np.pi) + np.cos(points[:, 1] * 2 * np.pi)

grid_x, grid_y = np.mgrid[0:1:100j, 0:1:100j]
grid_z = griddata(points, values, (grid_x, grid_y), method='cubic')

plt.imshow(grid_z.T, extent=(0,1,0,1), origin='lower')
plt.scatter(points[:,0], points[:,1], c=values, edgecolors='k')
plt.title('2D Cubic Interpolation')
plt.colorbar()
plt.show()

method: 'linear', 'nearest', 'cubic'

`RBFInterpolator`（任意次元・ラジアル基底関数補間）

from scipy.interpolate import RBFInterpolator

rbf = RBFInterpolator(points, values, kernel='thin_plate_spline')
z_rbf = rbf(np.stack([grid_x.ravel(), grid_y.ravel()], axis=-1))
z_rbf = z_rbf.reshape(100, 100)

plt.imshow(z_rbf.T, extent=(0,1,0,1), origin='lower')
plt.title('RBF Interpolation')
plt.show()

より柔軟でスムーズな補間が可能。
kernelの種類：'multiquadric', 'inverse', 'gaussian', 'linear', 'cubic', 'quintic', 'thin_plate_spline' など。

補間手法の使い分け

手法	特徴	向いている場面
`interp1d`	手軽・高速	等間隔・1次元時系列補間
`UnivariateSpline`	スムージング可能なスプライン	ノイズがあるデータ
`CubicSpline`	高精度・なめらか	物理シミュレーション・音声処理など
`griddata`	グリッド上で2D補間	地形マップ、画像補間など
`RBFInterpolator`	任意次元対応・柔軟	高次元データ補間、局所的構造