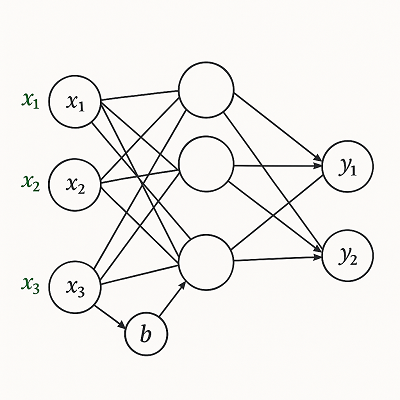
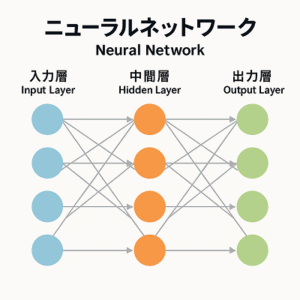
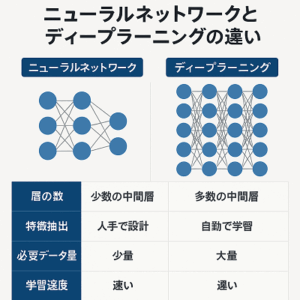
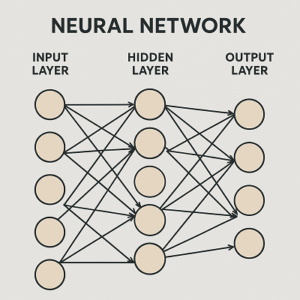
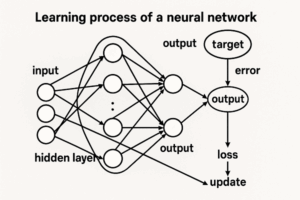
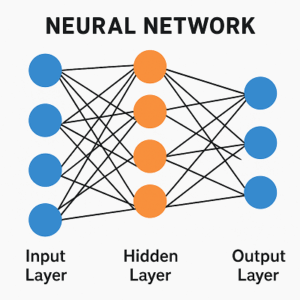
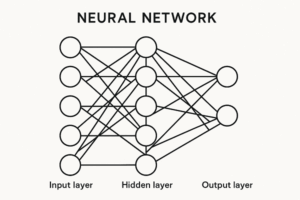
ニューラルネットワーク(Neural Network)は、人間の脳の神経細胞(ニューロン)を模した構造を持ちます。
その中で最も重要な要素のひとつが「重み(Weight)」です。
重みとは、入力信号が次の層のニューロンにどの程度影響を与えるかを決める係数のことです。
つまり、各入力情報に対して「どれをどれだけ重視するか」を数値的に表したものです。
重みの基本構造と数式
各ニューロンの出力は、複数の入力に重みを掛け合わせた線形結合と、バイアス(bias)項を加えたものから構成されます。
z=w1x1+w2x2+w3x3+...+bここで
- (x_i):入力データ
- (w_i):入力に対する重み
- (b):バイアス(出力の基準を調整する定数)
- (z):次の層へ渡される線形結合結果
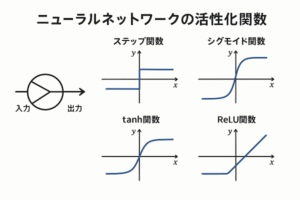
この値 (z) に活性化関数(Activation Function)を通して非線形性を導入することで、ネットワークはより複雑な関係を学習できます。
重みが果たす役割:入力の重要度を学習する
重みは、ネットワークが「どの入力要素をどれだけ重要視するか」を学習するためのパラメータです。
例
ある広告クリック予測モデルを考えましょう。
| 特徴量 | 説明 | 重み(学習前) |
|---|---|---|
| x1 | ユーザーの年齢 | 0.1 |
| x2 | 興味カテゴリ一致度 | 0.9 |
| x3 | 広告の表示頻度 | 0.4 |
学習が進むと、もし「興味カテゴリの一致度」がクリック率に最も影響するなら、重み (w2) が他の特徴より大きくなり、ネットワークはその特徴をより重視します。
重みの学習プロセス:誤差逆伝播法(Backpropagation)
重みは手動で設定されるのではなく、誤差逆伝播法(Backpropagation)によって自動的に最適化されます。
ステップの流れ
- 順伝播(Forward Propagation)
入力データをネットワークに通し、出力 (y’) を得る。 - 損失関数(Loss Function)で誤差を計算
出力 (y’) と正解 (y) の差を定量化。- 回帰:MSE(平均二乗誤差)
- 二値分類:Binary Cross-Entropy
- 多クラス分類:Categorical Cross-Entropy
- 逆伝播(Backpropagation)
各重みが誤差にどれだけ寄与したかを偏微分で求める。 - 勾配降下法(Gradient Descent)で重みを更新
学習率 (\eta) に基づいて重みを微調整。
この操作を数千〜数万回の反復で行い、最適な重みを求めていきます。
実務ではAdam、SGD with Momentum、AdamWなどの最適化手法がよく用いられます。
重みの初期化と学習の安定性
重みの初期値を適切に設定しないと、学習が不安定になったり、勾配が消失・爆発する問題が発生します。
主な初期化手法
| 手法 | 適用例 | 特徴 |
|---|---|---|
| Xavier(Glorot)初期化 | Sigmoid, tanhなど対称関数 | 層間の分散を均一化 |
| He(Kaiming)初期化 | ReLU, LeakyReLUなど非対称関数 | 勾配消失を抑制 |
加えて、Batch NormalizationやResidual Connection(残差接続)などの手法も、勾配の流れを安定化させます。
重みの正則化:過学習を防ぐ仕組み
重みが大きくなりすぎるとモデルが訓練データに過剰適合する(過学習)ため、正則化(Regularization)で抑制します。
代表的な正則化法
- L1正則化(Lasso)
→ 不要な特徴量の重みが0になりやすく、特徴選択に有効。 - L2正則化(Ridge)
→ 重み全体の大きさを滑らかに縮小し、モデルを安定化。
実装上は「L2正則化」と「weight decay(重み減衰)」が混用されますが、AdamWのように両者を分離して扱う手法が推奨されます。
重みの可視化と解釈
重みは単なる数値ではなく、学習過程の「知識の痕跡」です。
可視化することでモデルの挙動を直感的に理解できます。
- CNN(畳み込みニューラルネットワーク)では、初期層の重みは「エッジ」や「線」などの低レベル特徴を捉え、
深層では「形」「パターン」「顔」などの抽象概念を検出。 - Grad-CAMやIntegrated Gradientsなどを併用すると、特定の出力に対してどの入力領域に重みが集中したかを視覚的に分析できます。
実務での応用と「重みづけ」の考え方
重みの概念は、機械学習だけでなくマーケティング分析にも応用できます。
本質的には「重要な要素を数値的に強調すること」です。
マーケティング領域の例
| 分野 | 重みの解釈・応用例 |
|---|---|
| 広告配信最適化 | 各特徴(ユーザー属性、興味、過去行動)の重要度を重みとして学習。 |
| レコメンドエンジン | ユーザー嗜好ベクトルに重みを与え、関連性の高いコンテンツを提示。 |
| 顧客セグメンテーション | 特徴量をスケーリングや距離学習で重みづけし、クラスタリング精度を向上。 |
特にクラスタリングでは「重み付き距離」や「メトリック学習」により、より意味のあるグルーピングが可能になります
まとめ
| 項目 | 内容 |
|---|---|
| 重みとは | 入力要素の重要度を示すパラメータ |
| 学習法 | 誤差逆伝播と勾配降下で最適化 |
| 損失関数 | タスクに応じてMSEまたはクロスエントロピー |
| 初期化 | Xavier/He初期化で安定性確保 |
| 正則化 | L1/L2またはweight decayで過学習防止 |
| 可視化 | Grad-CAM・Feature Map解析など |
| 実務的意義 | 特徴の重要度学習、広告最適化、顧客分析などに応用可能 |
以上、ニューラルネットワークの重みづけについてでした。
最後までお読みいただき、ありがとうございました。