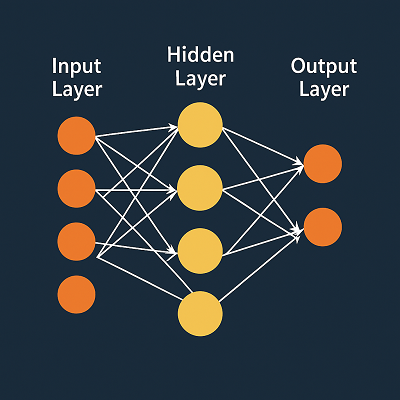
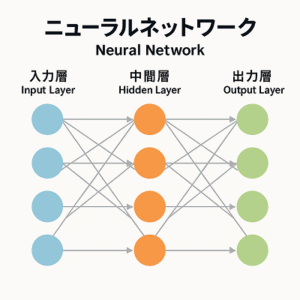
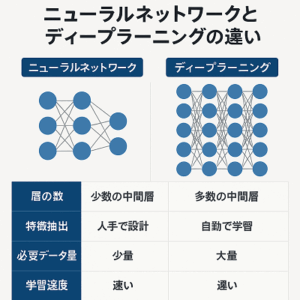
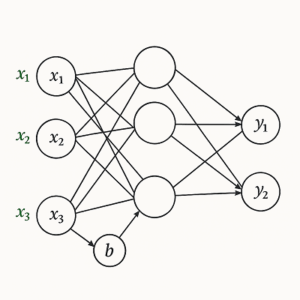
ニューラルネットワークの「バイアス(bias)」は、一見すると単なる定数項のように見えますが、モデルの表現力・学習効率・安定性を支える極めて重要なパラメータです。
重み(weight)が「入力の傾き」を決めるのに対し、バイアスは「関数の位置」を調整します。
これにより、モデルは入力空間の原点に縛られず、柔軟にデータを表現できるようになります。
数式で見るバイアスの役割
まず、1つのニューロン(ノード)の計算式を考えます。
y=f(w1x1+w2x2+⋯+wnxn+b)ここで
- (x_i):入力値
- (w_i):対応する重み
- (b):バイアス(定数項)
- (f(\cdot)):活性化関数(ReLU, sigmoid, tanh など)
この式における「+ b」がバイアスです。
もしこの項がなければ、ネットワークの線形変換は原点(0,0,…)を必ず通る線形写像に固定されてしまい、表現できる関数の自由度が大幅に制限されます。
バイアスの直感的理解
閾値(しきい値)のような働き
ニューロンは、入力の加重和がある値を超えたときに「発火」するように設計されています。
バイアスはその「発火する位置(閾値)」を調整する役割を持ちます。
たとえば線形モデルを考えると
y = wx + bここでバイアスがなければ、直線は必ず原点を通ります。
しかしバイアスを加えることで、直線を上下に移動でき、より多様な関数を表現できます。
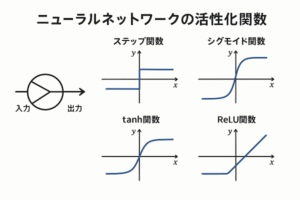
活性化関数のシフト
多くの活性化関数(例:sigmoid, tanh)は入力0付近で特徴的な出力を持ちます。
バイアスはこの関数の入力を平行移動し、ニューロンの出力範囲を柔軟にコントロールします。
f(x)=sigmoid(x)これにより、「入力が0でも出力が0.5ではなく0.9付近になるようにしたい」といった微調整が可能になります。
バイアスがないと起こる制約
バイアスが存在しない場合、ネットワークには次のような制約が生じます。
- 原点通過の制約:全ての線形写像が原点を通るため、データを十分に表現できない。
- 決定境界の柔軟性が失われる:分類問題では、分離境界の「位置」を調整できず、学習が不安定になる。
- 層を重ねても原点固定が残る:活性化関数を挟んでも、ネットワーク全体が原点に“錨付け”される構造的制約が残り、表現力が限定される。
つまり、非線形性自体は残るものの、ネットワークが表現できる関数の範囲(関数族)が狭くなってしまうのです。
実装上のポイントと応用知識
「bias trick」とは?
バイアスは、入力ベクトルに常に1を加える拡張によって表現できます。
y=W[x;1]この形にすると、バイアスも「重み行列の一部」として扱えるため、理論的にも実装的にも便利です。
Batch Normalizationとの関係
BatchNormやLayerNormは平均を引いて正規化するため、直前の層のバイアスは冗長になります。
そのため、実装では「bias=False」として計算を省くのが一般的です。
例
nn.Linear(in_features, out_features, bias=False)
nn.BatchNorm1d(out_features)
ReLU系活性化関数と初期バイアス
ReLU(負の値を0にする)では、初期状態で全ての前活性が負だと「死にユニット」が発生します。
これを防ぐために、初期バイアスを小さく正に設定すると、学習初期の安定性が向上することがあります。
CNNにおけるバイアス
畳み込みニューラルネットワーク(CNN)では、出力チャネルごとに1つのバイアスが存在します。
これはフィルタの全ての空間位置で共有され、特徴マップ全体の「出力の基準値」を調整します。
ロジスティック回帰におけるバイアスの意味
ロジスティック回帰では、バイアス (b) は「事前対数オッズ(intercept)」として働きます。
これはデータのクラス分布の偏りを補正する役割を持ち、確率出力のキャリブレーションに直結します。
理論的背景:普遍近似定理とバイアス
多くの「ニューラルネットワークの普遍近似定理(universal approximation theorem)」は、バイアスを含むネットワークを前提としています。
バイアスのないネットワークは原点を固定するため、任意の連続関数を近似する保証が成立しません。
したがって、理論的にもバイアスは表現力を保証する必須要素なのです。
現代モデルにおける設計上の傾向
- Transformer系モデルでは、一部の線形層(例:QKV projectionなど)でバイアスを省略する設計も見られます。
これはLayerNormや残差接続の存在により、バイアスの寄与が小さいためです。 - 一方で、小規模ネットワークや非正規化層を多用する構造では、バイアスを残した方が学習の安定性が向上する傾向があります。
まとめ
| 観点 | 内容 |
|---|---|
| 定義 | 各ニューロンの前活性に加わる定数項 |
| 数式 | ( y = f(Wx + b) ) の (b) がバイアス |
| 役割 | 決定境界や活性化関数の位置を平行移動し、柔軟な表現を可能にする |
| 無い場合の問題 | 原点通過の制約により表現力が低下、学習が不安定化 |
| 学習 | 勾配降下法で自動更新される |
| 実務的注意 | BN後では冗長、ReLU系では初期値が重要、CNNでは出力チャネル単位で存在 |
以上、ニューラルネットワークのバイアスの役割についてでした。
最後までお読みいただき、ありがとうございました。